Example 1. The trivial bundle with total space B × ℝn, with projection map π(b,x) = b, and with the vector space structures in the fibers defined by
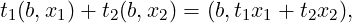
will be denoted by ϵBn.
In algebraic topology, we wish to use tools from abstract algebra to help us classify topological spaces up
to homomorphism by way of algebraic invariants. One way to do this is through chracteristic classes. In
this paper, we will give a basic roadmap to an axiomatic approach to Stiefel-Whitney classes. We will first
study vector bundles and then cohomology groups which will then be combined to discover characteristic
classes. After giving some applications and examples, mainly about Stiefel-Whitney numbers, we
hope to motivate the study of other characteristic classes such as the Chern or Pontrjagin
classes.
Vector bundles are important to the study of topological spaces as they give a precise idea about families
of vector spaces parametrized by some other space. Through their applications, we can find deeper
properties about the spaces themselves and also maps between spaces. (maybe something on finitely
generated projective modules)
Definition 1. A real vector bundle ξ over B consists of the following:
A topological space E = E(ξ) called the total space;
A continuous map π : E → B called the projection map;
For each b ∈ B, the structure of a vector space over the real numbers in the set π-1(b).
We can think of vector bundles visually as some bridging structure defined by the projection map from one space to another. To help digest this definition, let us give some simple examples starting off with the trivial bundle.
Example 1. The trivial bundle with total space B × ℝn, with projection map π(b,x) = b, and with the vector space structures in the fibers defined by
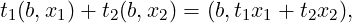
will be denoted by ϵBn.
Example 2. The tangent bundle τM of a smooth manifold M has the total space DM consisting of all pairs (x,v) with x ∈ M and v tangent to M at x. The projection map is defined by π(x,v) = x and the vector space structure in π-1(x) is defined by
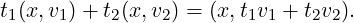
vector fields are sections of vector bundles
Example 3. The normal bundle of a smooth manifold M ⊂ ℝn has the total space E ⊂ M × ℝn, which is the set of all pairs (x,v) such that v is orthogonal to the tangent space DMX. The projection map and the vector space structure is similarly defined as the tangent bundle.
Below is a hand-drawing from Milnor-Stasheff [MilnorStasheff] to help visualize these examples.

There is much to learn about vector bundles, but for the sake of this paper, we will give only a fraction of the important definitions.
Definition 2. Two vector bundles, ξ and η, are isomorphic ξ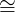 η if there exists a homeomorphism
η if there exists a homeomorphism
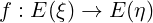
between the total spaces which maps each vector space Fb(ξ) isomorphically onto the corresponding vector space Fb(η).
To prove this theorem, we first require the notion of a cross-section.
Definition 3. A cross-section of a vector bundle ξ with base space B is a continuous function
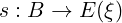
which takes each b ∈ B into the corresponding fiber Fb(ξ). A common example is the cross-section of the tangent bundle of a smooth manifold M, which is usually called a vector field on M.
Definition 4. A cross-section is nowhere zero if s(b) is a non-zero vector of Fb(ξ) for each b. The cross-sections s1,…,sn are nowhere dependent if for each b ∈ B, the vectors s1(b),…,sn(b) are linearly independent.
Proof. Since a trivial ℝ1-bundle has a cross-section that is nowhere zero, we wish to show that γn1 has no such cross-section. Let
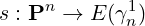
be any cross-section, and consider the composition
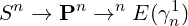
carrying each point x ∈ Sn to some pair
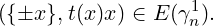
t(x) is a continuous real-valued function of x with the property that t(-x) = -t(x). Since Sn is connected, by the intermediate value theorem t(x0) = 0 for some point x0. Thus, s({�x0}) = ({�x0},0), and so γn1 is not trivial. □
Now, we further motivate the importance of vector bundles with some significant results.
Theorem 2. An ℝn bundle ξ is trivial if and only if ξ admits n cross-sections s1,…,sn which are nowhere dependent.
Lemma 1. Let ξ and η be vector bundles over B and let f : E(ξ) → E(η) be a continuous function which maps each vector space Fb(ξ) isomorphically onto the corresponding vector space Fb(η). Then f is necessarily a homeomorphism. Hence ξ is isomorphic to η.
With a great phonetic similarity to homology, cohomology groups also share similar axioms to homology
groups. However, the benefit of computing cohomology groups is that the natural ”cup” product of
cohomology groups provides an additional algebraic structure that can be more useful. Let us first begin
with some definitions.
Definition 5. Given groups (A,∘) and (B,⋅), a group homomorphism is a function h : A → B such that for all x,y ∈ A, h(x ∘ y) = h(x) ⋅ h(y).
The building blocks for these homology and cohomology groups lies in connecting spaces through homomorphisms in two similar, yet distinct manners.
Definition 6. A chain complex (A∙,d∙) is a sequence of abelian groups or modules …,A0,A1,… connected by group homomorphisms (called boundary operators or differentials) dn : An → An-1 such that the compositions of any two maps is the zero map (dn ∘ dn+1 = 0).
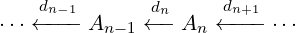
Example 4. A1 = (ℤ,+) is the group of integers under addition
A0 = (ℤ∕2ℤ,+) is the cyclic group of integers mod 2 under addition
An = 0 is the zero group for all n ⁄∈{0,1}. d1(x) = x (mod 2)
dn(x) = 0 for all n≠1
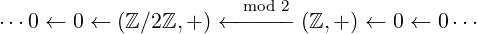
Since d2 ∘ d1(x) = d1(0) = 0, and dn ∘ dn+1 = 0 by inspection for all other n, this is clearly a chain complex.
The dual of a chain complex is appropriately named the cochain complex.
Definition 7. A cochain complex (A∙,d∙) is a sequence of abelian groups or modules …,A0,A1,… connected by homomorphisms dn : An → An+1 such that the compositions of any two maps is the zero map (dn+1 ∘ dn = 0).
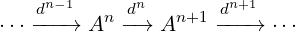
Example 5. For any p ∈ ℤ≥2
A0 = (ℤ,+)
A1 = (ℤ,+)
A2 = (ℤ∕pℤ,+)
An = 0 for all n ⁄∈{0,1,2}
d0(x) = p × x
d1(x) = x (mod p)
dn(x) = 0 for all n ⁄∈{0,1}
Remark 1. Here are some clarifying remarks about (co)chain complexes:
They are infinitely long in both directions. If you call a (co)chain complex finitely long, then you are suggesting that everything that comes before and after in the chain is the zero group.
As a consequence, they have no beginning or end unless you are not counting the infinitely long chains of zero groups that come before or after.
(Co)chain groups don’t need to have the zero group at all! They can be infinitely long and just have non-zero groups that extend in both directions.
Now, we show how these groups can be computed in order to study topological spaces.
Example 6. Using the cochain complex example from above, we see that the kernel of d1(x) = x (mod p) is just the set pℤ ⊂ ℤ. The image of d1(x) = px is pℤ. That means the quotient group H1 is
Definition 10. The standard n-simplex is the convex set Δn ⊂ ℝn+1 consisting of all (n + 1)-tuples (t0,…,tn) of real numbers with
Simplices show up quite often in the study of geometric structures, and their visualizations are very friendly.
Example 8. The 1-simplex consists of the line segment connecting the points (1,0) and (0,1) including the endpoints.
Now, let us build some fundamental concepts for characteristic classes.
Definition 11. A singular n-simplex in a topological space X is a continuous map σ from the standard n-simplex Δn to X, written σ : Δn → X. The i-th face of a singular n-simplex σ is the singular (n-1)-simplex
where the linear imbedding ϕi : Δn-1 → Δn is defined by
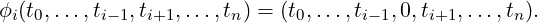
We denote the set of all n-simplices in X as Sinn(X). Note that Sinn(X) = 0 for n < 0.
Definition 12. The singular chain complex of a topological space X, denoted (C∙(X),d∙) is
created where Cn(X) is the free abelian group created by the basis Sinn(X) and dn : Cn(X) →
Cn-1(X) is dn(σ) = ∑
i(-1)iσ∣![[v0,⋅⋅⋅ ,ˆvi,⋅⋅⋅ ,vn]](main18x.png) .
.
Definition 13. The nth singular homology group is the nth homology group of the nth singular chain complex.
Definition 14. The cochain group Cn(X;Λ) is defined to be the dual module HomΛ(Cn(X;Λ),Λ) consisting of all Λ-linear maps from Cn(X;Λ) to Λ.
Definition 15. The coboundary of a cochain c ∈ Cn(X;Λ) is defined to be the cochain δc ∈ Cn+1(X;Λ) whose value on each (n + 1)-chain a is determined by the identity
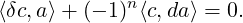
We can think of Bn(X;Λ) as the coboundary of the cochain group Cn-1(X;Λ) which is a subset of Cn(X;Λ).
Remark 2. Cohomology groups are determined algebraically by homology groups. Here are the steps to do so:
Take a chain complex of singular, simplicial, or cellular chains.
Take the homology groups of the chain complex, kerd∕im d.
Replace the chain groups Cn by the dual groups Hom(Cn,G) and the boundary maps d by their dual maps δ.
Then, the cohomology groups are kerδ∕im δ.
Finally, we have a sufficient understanding to grasp what characteristic classes are. Primarily, we are
interested in various characteristic classes because they are used to measure vector bundles of a
topological space using cohomology. To do this, we map the principal bundles of a topological space X to
its cohomology classes. This mapping can be done in many different ways, but in this paper we will look
at the Steifel-Whitney Classes.
Definition 17. Hi(B;G) denotes the i-th singular cohomology group of topological space B with coefficients in G.
For the Stiefel-Whitney classes, we give an axiomatic approach.
Axiom 1. To each vector bundle ξ there corresponds a sequence of cohomology classes
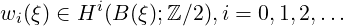
called the Stiefel-Whitney classes of ξ. The class w0(ξ) is equal to the unit element
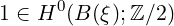
and wi(ξ) equals zero for i greater than n if ξ is an n-plane bundle.
Consequently from Axiom 2, we have the following.
Proposition 2. If ϵ is a trivial vector bundle, then wi(ϵ) = 0 for i > 0. This is because there exists a bundle map from ϵ to a vector bundle over a point.
As a consequence of the Whitney Product theorem and the naturality axiom,
Proposition 4. If ξ is an ℝn-bundle with a Euclidean metric which possesses a nowhere zero cross-section, then wn(ξ) = 0. If ξ possesses k cross-sections which are nowhere linearly dependent, then
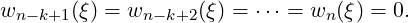
Example 9. Using the standard imbedding of Sn ⊂ ℝn+1, the normal bundle v is trivial. Let τ be the tangent bundle of the unit sphere Sn. Then by the Whitney Product theorem, w(τ)w(v) = 1 and since v is trivial, w(v) = 1. Thus, w(τ) = 1. Therefore, the class w(τ) = w(Sn) is equal to 1, and τ is indistinguishable from the trivial bundle over Sn by Steifel-Whitney classes.
Theorem 3. The Whitney sum τ ⊕ϵ1 is isomorphic to the (n + 1)-fold Whitney sum γn1 ⊕γn1 ⊕
 ⊕ γn1. Hence the total Stiefel-Whitney class of Pn is given by
⊕ γn1. Hence the total Stiefel-Whitney class of Pn is given by
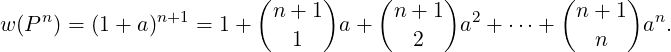
Definition 18. A smooth map f : M → N between smooth manifolds is called an immersion if the Jacobian
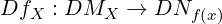
maps the tangent space DMX injectively for each x ∈ M.
If a manifold M of dimension n can be immersed in the Euclidean space ℝn+k, then the Whitney duality theorem implies that the dual Stiefel-Whitney classes are zero for i > k.
Let Pn denote the real projective space in n dimensions.
6.1. Stiefel-Whitney Numbers. Stiefel-Whitney numbers allows for a comparison between the Stiefel-Whitney classes of two different manifolds. In studying manifolds, we consider the collection of all possible Stiefel-Whitney numbers. We say that two different manifolds M and M′ have the same Stiefel-Whitney numbers if
![r1 rn r1 r1 ′
w1 ⋅⋅⋅w n [M ] = w1 ⋅⋅⋅w 1 [M ]](main29x.png)
for every monomial w1r1 wnrn of total dimension n.
wnrn of total dimension n.
Theorem 5. If B is a smooth compact (n + 1)-dimensional manifold with boundary equal to M, then the Stiefel-Whitney numbers of M are all zero.
Theorem 6. If all the Stiefel-Whitney numbers of a manifold M are zero, then M can be realized as the boundary of some smooth compact manifold.
Corollary 1. Two smooth closed n-manifolds belong to the same cobordism class if and only if all of their corresponding Stiefel-Whitney numbers are equal.
To close, vector bundles themselves are quite fascinating, however it’s when we begin to construct groups
with vector bundles that we see these magical algebraic properties of manifolds arise. Cohomology groups,
while quite novel at first, do become a natural consideration. This is because we extract new relationships
between spaces by way of the algebraic structure of cohomology classes of vector bundles. After the
Stiefel-Whitney classes, there are many paths for further research after this paper. For example,
one can explore vector bundles and manifolds in ℂ, which gives the added benefit of being
algebraically closed. Then, one could study Chern classes and Chern numbers of a compact complex
manifold.